銀行內評模型構建的全流程指導：違約損失率模型

作者：相信未來

來源：泓策投研手札（ID：FinanceBao）

評級是藝術，但你廢掉另一只腿科學，直接和我開聊藝術和分析框架我就難以信服了，兩者不矛盾，你為什么不和我聊聊科學？前述文章中談及了數據治理問題(大數據信用風險管理操作手冊)，以及內評模型驗證問題(內部評級模型驗證方法全解析)，本文則詳細敘述銀行內評模型建模的全流程（債券評級模型有自身特征），歡迎來懟。

違約損失率，也就是當客戶發生違約后，債項損失的程度，等于1-回收率。《巴塞爾協議》強調“估計違約損失率的損失是指經濟損失”，而不是會計上的賬面損失。經濟損失要考慮回收成本和資金的時間價值，也就是利用合適的折現率計算禍首現金流的現值。所以《巴塞爾協議》下的違約損失率(LGD)為：

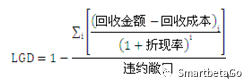
計算歷史LGD的三個關鍵：回收現金流(有效催收窗口)、回收成本、折現率。

• 數據收集和變量構造

LGD模型構建一直是銀行的難點，關鍵障礙在于LGD的數據缺失相當嚴重。LGD建模所需要數據可分為兩部分：因變量和自變量計算所需要的數據。違約概率(PD)模型的數據缺失主要為自變量計算所需要數據的缺失，因變量(即違約與否的判斷)數據質量相對較好，而LGD模型這兩方面的數據缺失都相當嚴重。

歷史LGD的計算數據，重點在于回收現金流、回收成本、折現率。關于回收現金流，各行都有催收臺賬，但是很少有銀行在IT系統記錄了詳細準確的交易明細，成本分攤更是商業銀行的軟肋，準確地估計某個機構、某個時段、某個產品的回收成本幾乎是不可能的。大型商業銀行已經上線了標準催收、ERP等系統，這方面的情況有所改善。

自變量數據，包括債項類型、債項的優先級別、抵(質)押品、抵債資產的優先求債權、破產相關法律因素、行業因素、違約概率、商業周期、信貸歷史、宏觀經濟等方面，其中，商業銀行對于抵(質)押品的管理一直比較薄弱，數據積累也非常差，各大商業銀行已經開始已經建設抵(質)押品市值重估和管理系統，數據情況得到改善。

穆迪的LossCalc?模型(Guptonand Stein, 2002)包括了債務類型和優先級、資本結構、行業、宏觀經濟四個方面的九個自變量。

         穆迪LossCalc(TM)模型變量

• 模型分組和樣本選擇

違約損失率LGD模型的分組基本上與客戶違約概率評級模型的分組原則比較類似，一般可以從行業、規模、區域、產品等維度進行分組，具體應該選擇幾個維度，在每個維度如何分組，應該考察經濟學直覺、業務管理情況、數據來源、統計分析等幾個方面的情況。

違約損失率LGD模型必須要進行非違約賬戶和違約賬戶的分組，因為已經違約的客戶包括了逾期后回收的更新數據，信息量遠大于非違約賬戶，可以構造更多的自變量，預測也更為準確。

在非違約賬戶和違約賬戶分組中，LGD模型建設都只使用違約樣本，但是觀察期和表現期的構造不一致。非違約賬戶分組中，所有樣本在觀察點之前還沒有發生違約，而在表現期內都發生違約，發生違約的賬戶回收率取決于有效催收窗口的分析，所以LGD模型的建設對于歷史數據的時間長度要求比較高。

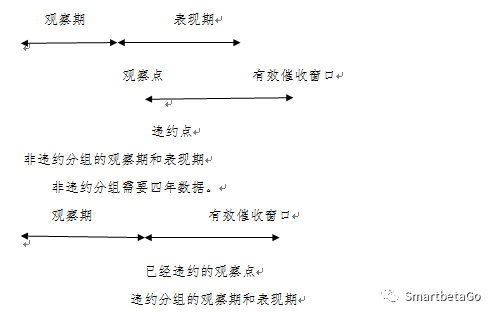
違約賬戶分組中，所有樣本在當前觀察點之前都已經發生違約，有效催收窗口在觀察點之前已經開始，需要三年數據。

• LGD分布特征

  1、Beta 分布

  

• 

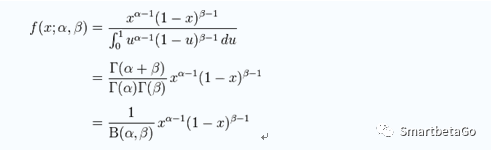
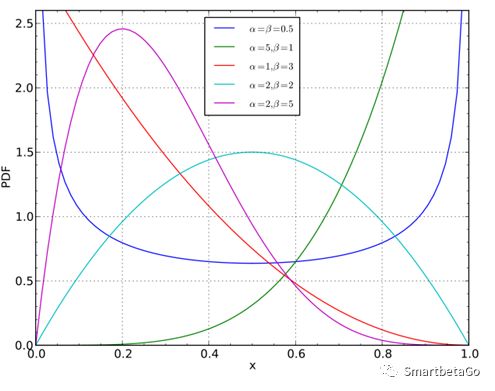
2、穆迪通過實證認為回收率服從Beta分布。

首先，回收率分布區間為[0,1]

Beta分布的形狀隨著兩個參數的變化而呈現很大的差異，也能很好地擬合偏峰厚尾的情況。

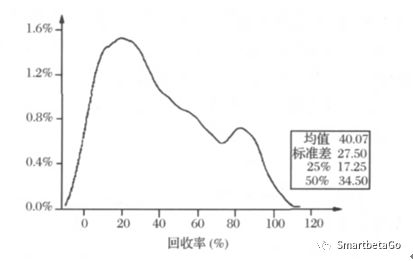
Ｍｏｏｄｙ公司１９７０－２００２年第二季度間所有

債券和貸款回收率

LGD呈現的雙峰分布(Bimodal Distribution)，商業銀行的信貸業務，雙峰的情況比較嚴重。直覺上也比較容易理解，如果債務人主觀上愿意還錢，無論時間長短，最終回歸換大部分的借款，即違約損失率LGD比較低，呈現為低端的峰；如果債務人主觀上沒有意愿還錢，既然是違約，不如違約徹底，即違約損失率LGD比較高，呈現高端的峰。

特別對于中國商業銀行，因為受國內壞賬核銷等法規和信用環境的影響，雙峰分布更為極端，LGD取值0和1的情況占比非常大，也就是說，很多債務在催收后能全額還款，而有些債務則一分錢都沒能回收。

雙Beta函數的密度函數為

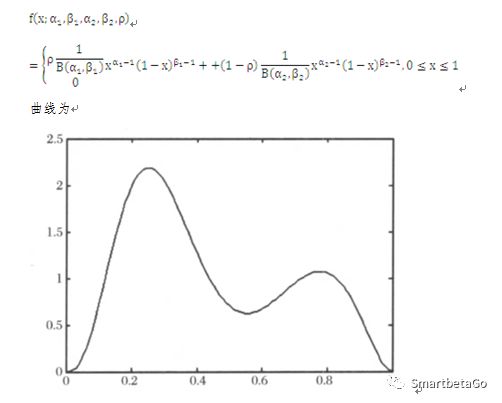
對于中國的商業銀行，因為受到國內壞賬核銷等法規的影響，雙峰分布更為極端，LGD取值為0和1的情況占比非常大：很多債務在催收后能全額還款，有些債務則分文收不回來。

• 模型方法論

理論上，沒有絕對最優的模型方法論，其選擇依賴于研究對象的數據結構和數據特性。違約損失率LGD數據的特點是：

1. LGD取值局限于[0,1]，實證研究表明其分布為貝塔分布或雙峰分布，總之不是正態分布，不適合使用線性回歸模型。客戶評級模型常用的Logistic回歸是半參數方法，對于分布要求并不要個，能否使用LGD模型呢？

2. LGD取值在[0,1]連續，Logistic回歸應用于分類問題，需要因變量離散變量，無法直接應用。

根據違約損失率LGD數據的特點，介紹三種模型方法：穆迪LossCalc?模型、構造樣本Logistic回歸、決策樹。

(1)     穆迪的LossCalc?模型

穆迪的違約損失率LossCalc?模型基于回收率為因變量展開，由于回收率=1-LGD，所以無論是LGD還是回收率為因變量，沒有什么本質區別。

(1-1)  logistic模型

穆迪的違約損失率LossCalc?模型中迷你模型類似穆迪違約概率模型RiskCal的處理，即通過單變量分析得到自變量到歷史平均LGD的轉化函數。

(1-2)   分布轉化

在回收率符合貝塔分布的情況下，可以通過分布轉化函數將貝塔空間下的回收率R轉化成正態空間下的回收率

在正態空間下，可以采用線性回歸：

其中，Betadist(R)代表Beta分布函數

      為迷你模型的輸出結果作為回歸模型的輸入

(2)     構造樣本Logistic回歸

LossCalc?模型方法在LGD取值比較連續的時候比較有效，但是對于中國的商業銀行業LGD分布在1和0點過多的情況，適用性有限。

如果LGD取值0和1比重非常高，可以采用Logistic回歸方法，對于其中在區間(0,1)的值，可以采用如下構造樣本的處理方法：

(2-1)   四舍五入法。顧名思義，就是LGD取值大于等于0.5的時候取值1，小于0.5的時候取值0.

(2-2)  樣本權重法。四舍五入法的處理有點粗糙，只有雙峰現象明顯，LGD在區間(0,1)取值很少的時候才使用。樣本權重法則精細一些，例如對于LGD取值為0.6的樣本，構造LGD分別等于1和0的兩個樣本與其對應，然后在模型訓練中，LGD=1的樣本權重為0.6，LGD=0的權重為0.4。

(2-3)  虛擬樣本法。例如對于LGD取值為0.6的樣本，分別構造自變量形同的6個LGD等于1,4個LGD等于0的樣本；對于LGD取值為1和0的樣本，則需要負值10倍，以保證合理的樣本權重。虛擬樣本方法效果與樣本權重法一致。

(3)     決策樹

決策樹屬于非參數法，對于數據分布、數據類型都沒有嚴格要求，比較適合處理LGD模型這種特殊情況。而且決策樹方法也非常直觀，邏輯判斷過程在樹結構中一目了然，易于業務人員接受。

注：文章為作者獨立觀點，不代表資產界立場。

題圖來自 Pexels，基于 CC0 協議

本文由“泓策投研手札”投稿資產界，并經資產界編輯發布。版權歸原作者所有，未經授權，請勿轉載，謝謝！

原標題： 銀行內評模型構建的全流程指導（五）：違約損失率模型